みなさんこんにちは。このブログを書いている東急三崎口です。
この記事では、半導体を学ぶときに必ず出てくるエネルギーバンドについて、PN接合を作った時になぜ曲がるのかを簡単に解説していきます。
PN接合を作ると、接合部分でバンドが曲がるのは当たり前のように書いてあることが多いですが、一応数式で理解することができます。
初心者向けの本では詳しい数式は省略されていることが多いですが、「なぜ?」という点を明らかにするためにあえて数式に寄せて書いていきます。
バンドはなぜ曲がるのか
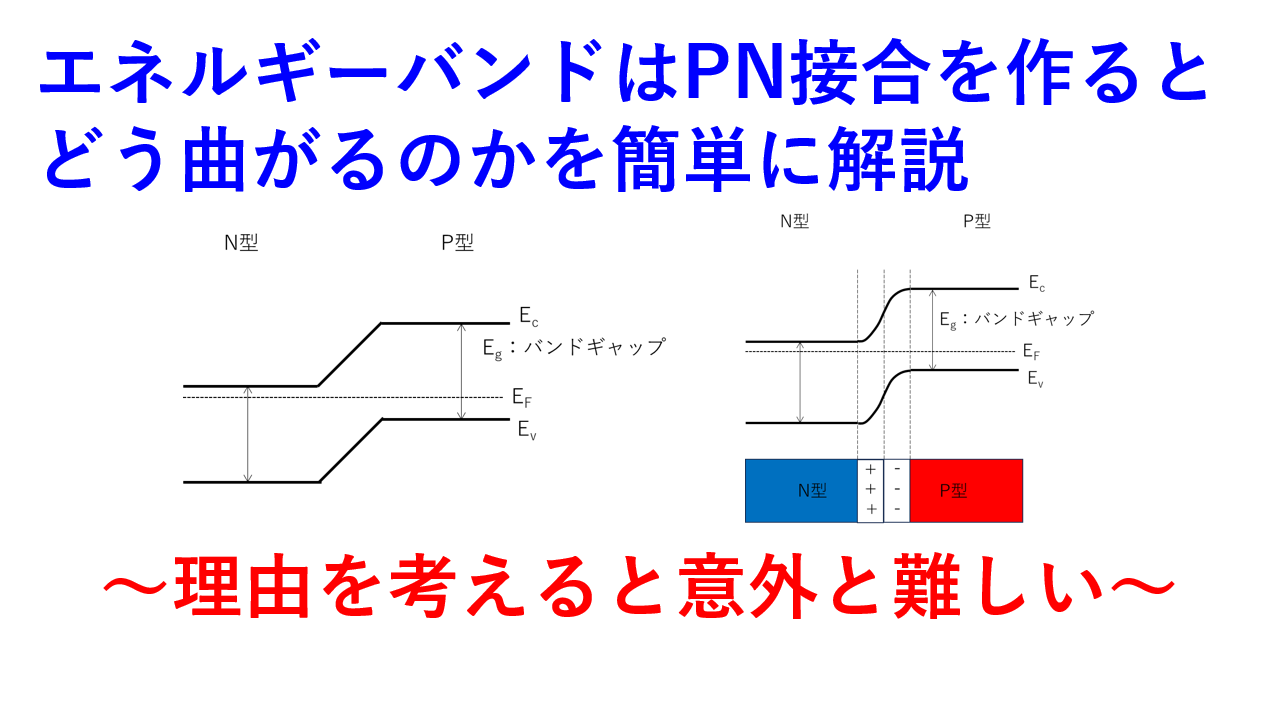
みなさんが見たことがあるPN接合のバンド図は、こんな形をしているのではないでしょうか。(この図は、少し違う部分がありますが、そこはのちほど書きます。)
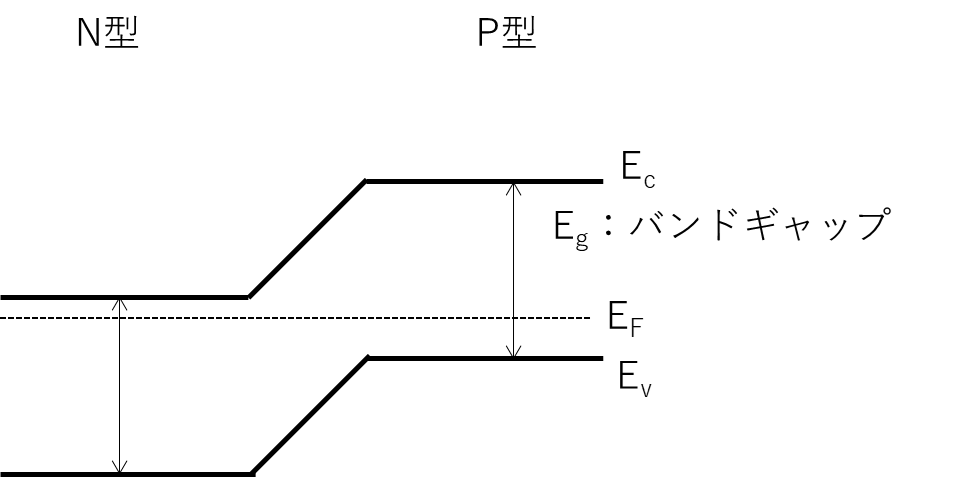
シリコンのPN接合だとすると、上側にEc(伝導帯)、下側にEv(価電子帯)、真ん中にEF(フェルミ準位)があって、EcとEvが曲がっているのがよくある形だと思います。
フェルミ準位をどう定義するかは、立ち位置によって色々な作法がありますが、ここでは半導体内での電位差(電圧)と考えることにします。
熱平衡状態の半導体中では電位差は生じないので、全ての場所でフェルミ準位は一定になります。(温度差つけたら話は別です。温度勾配に従って電位差が生じます。)
なぜバンドが曲がるのか?という問いに対する答えは、フェルミ準位を一定だと考えるとEc・Evを曲がっていえると考えた方が都合がいいからということになります。
PN接合した場合を考えてみる
わかったようなわからないような説明なので、実際にPN接合を作った場合のことを考えてみます。
簡単のために、P型・N型ともに同じキャリア濃度だったとしましょう。
N型半導体の中には、電子が自由に動けるキャリアとして存在します。また、電子をキャリアとして出した不純物は、+にイオン化しています。
P型半導体の中には、ホールがキャリアとして存在します。また、ホールをキャリアとして出した不純物は-にイオン化しています。
N型はマイナスの電荷をもつ電子がキャリアで、P型はプラスの電荷をもつホールがキャリアのイメージがありますが、イオン化している不純物の極性は逆になっています。(ここが要注意です。)
では、P型とN型を接合してみましょう。簡単に図にすると、こんな感じです。(磁石みたいになってしまいました・・・)

さて、接合した瞬間はこれでいいんですが、N型には電子が、P型にはホールがそれぞれ自由に動けるキャリアとして存在します。
自由に動けるということは、濃度勾配に応じて流れていってしまいます。N型の領域にはホールが無く、P型の領域には電子が無いので、N型領域の電子はP型側へ、P型領域のホールはN型側へ流れます。
ここで、注意したいのが、自由に動けるキャリアは動きますが、シリコン中にあるイオン化した不純物は動くことができないということです。
この時にPN接合直後の状態からどう変わったのかを考えると、教科書的にはこんな図になります。

バンド図で示すと、こんな感じです。
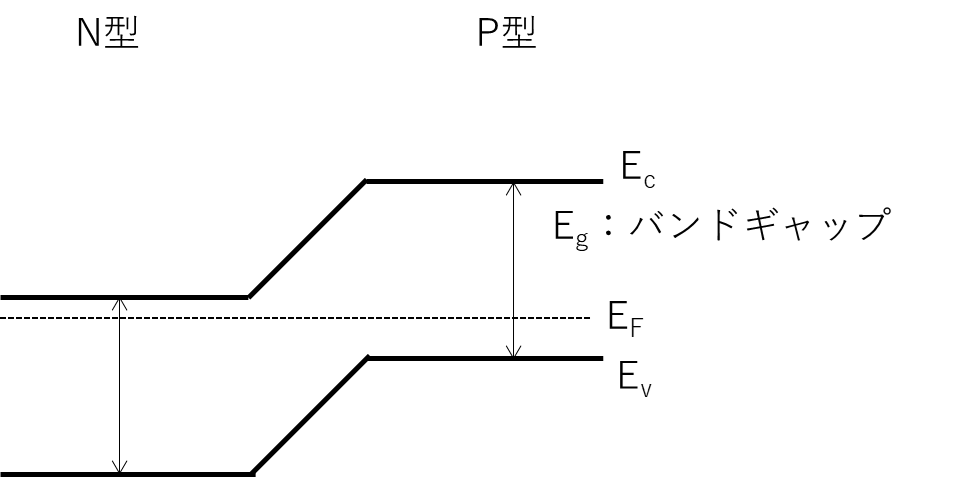
自由に動けるキャリアが、濃度勾配に従って拡散しきったあと、自由に動けない不純物のイオンの電荷が残るので、そこに電界が生じてバンドが曲がりますという説明です。
この時に、フェルミ準位が一定なのは、キャリアの拡散による拡散電流とイオン化した不純物によってつくられた電界による電流が釣り合うので、全体としては電流が流れない状態が実現できているからです。
N型とP型の間に物理的な壁があるわけではないんですが、電子がP型側に拡散しようとしても、濃度勾配による拡散の力と同じだけの電界が生じているので、電子はP型側にこれ以上拡散できない状態になっています。
P型側にいるホールから見ても、全く同じことが起こっています。
私は、一番最初にPN接合を学んだ時には、PN接合を作った時に拡散電流とイオン化した不純物によってつくられた電界がつりあって云々という説明がよくわからなかったんです。
ただ、正直なことを言うと、これはこういうもんだと思った方が早いです。
マクスウェル方程式が登場
PN接合を作ると、バンドが曲がりますという説明はよく描いてあります。前置きが長くなりましたが、今回の本題はここからです。
EcとEvは厳密に考えると、どんな曲線or直線になるのか?という話です。
適当に曲がっているように描けばそれっぽく見えるんですけど、実はPN接合のバンドの曲がりを直線で描くのは間違いです。
このことをちゃんと考えるには、マクスウェル方程式を知らないといけません。(マクスウェル方程式については、EMANの物理学でわかりやすく解説されているので、こちらのページがおすすめです。)
PN接合のバンドの曲がりを考えるときに使うのは、「divD=ρ」という式です。
ρは電荷密度です。PN接合のところでρとして考えるのは、シリコン中のイオン化した不純物の持つ電荷です。(図中で+,-としてあらわされているところです。)
PN接合を一次元的に考えると、divD=ρという式はdD/dx=ρと書けます。
ここで、Dは電束密度を表していて、D=εEと書けます。(εは誘電率、Eは電界です。)
さて、嫌になってきましね。
とりあえず、dD/dx=ρという式はdE/dx=ρ/εと書き直すことができます。
ρがxに依存しない定数だったら話は早いんですが、xによって変わるので少し考えないといけません。
さきほどPN接合した領域のρを考えて見ると、このようになります。
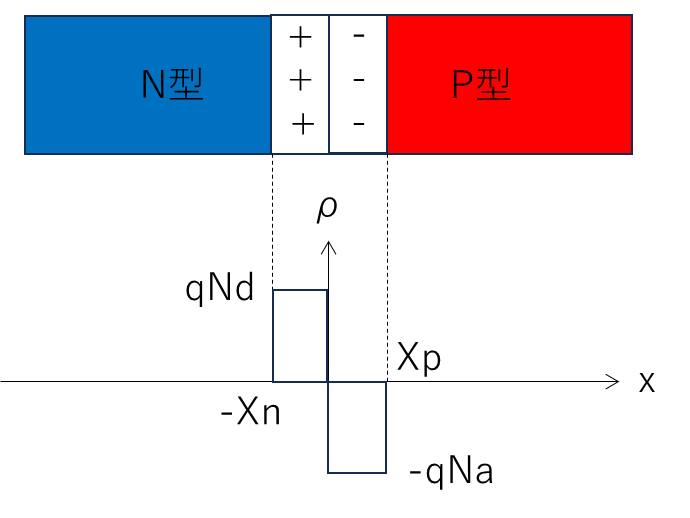
NdはN型領域の不純物密度、NaはP型領域の不純物密度で、Xn,XpはN型・P型それぞれのキャリアがいなくなって不純物イオンによる電界が生じている領域の距離としています。
キャリアが拡散しきって、不純物イオンによる電荷が生じている領域のことを、空乏層と呼びます。
このようにρを整理すると、ρは2つに分かれます。
・ρ=qNd (-Xn<x<0)
・ρ=-qNa (0<x<Xp)
そうすると、dE/dx=ρ/εの式は3つに分けられます。
・dE/dx=qNd/ε (-Xn<x<0)
・dE/dx=-qNa/ε (0<x<Xp)
ここで出した式は、微分系のマクスウェル方程式と呼ばれるものになります。
とりあえず、Eがどんな形になるのかそれぞれの場合で見ていきましょう。
dE/dx=qNd/ε (-Xn<x<0)の場合は、簡単な微分方程式として解けます。
E=(qNd/ε)x+(定数)となります。
この時、境界条件としてx=-XnのところではE=0となるので、(定数)=-(qNd/ε)Xnとなります。
定数も含めてEを表すと、
E=(qNd/ε)x-(qNd/ε)Xn=(qNd/ε)×(x-Xn)となります。
dE/dx=-qNa/ε (0<x<Xp)の場合も同様に、簡単な微分方程式として解くことができて、
E=-(qNa/ε)x+(定数)となります。
この時も、境界条件としてx=Xpの時にE=0となるので、定数を書き表すと、
(定数)=(qNa/ε)Xpとなり、
E=-(qNa/ε)×(Xp-x)となります。
※ここで出てくる微分方程式については、高校の数Ⅲか大学の初等数学でやるものです。詳しく知りたい方は、EMANの物理学のこちらのページを読んでみてください。
さて、エネルギーバンドで描かれているのは、電位(φ)です。
電界(E)と電位(φ)は、このような関係があります。(一次の場合。)
E=-dφ/dx
では、先ほど求めたEからφを求めてみましょう。
dE/dx=qNd/ε (-Xn<x<0)の場合は、E=(qNd/ε)x-(qNd/ε)Xnだったので、
(qNd/ε)x-(qNd/ε)Xn=-dφ/dxとなります。
φについて解くと、φ=-(qNd/2ε)x2+(qNd/ε)Xn・x+(定数1)です。
dE/dx=-qNa/ε (0<x<Xp)の場合も同様に、
φ=(qNa/2ε)x2-(qNa/ε)Xp・x+(定数2)です。
そして、φの基準としてはx=-Xnでφ=0とすると、定数1と定数2は0と置くことができます。
上記の式から、2つの領域のφはこのように書けます。
φ=-(qNd/2ε)x2+(qNd/ε)Xn・x (-Xn<x<0)
φ=(qNa/2ε)x2-(qNa/ε)Xp・x (0<x<Xp)
それでは、このようにして出てきたφを図に表してみましょう。式は、2つともxについての簡単な二次関数になっているので、図に描くには簡単です。
※二次関数のグラフは高校数学の数Ⅰで出てくる範囲なので、解説は省略しています。グラフのイメージがつかめない方は、放物線を描くと思ってもらえれば大丈夫です。詳しい内容は、こちらのリンク先を見れば十分です。
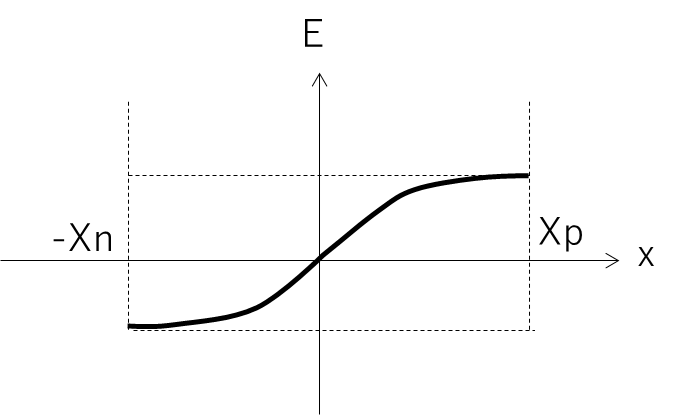
図にしてみると、こんな形になります。
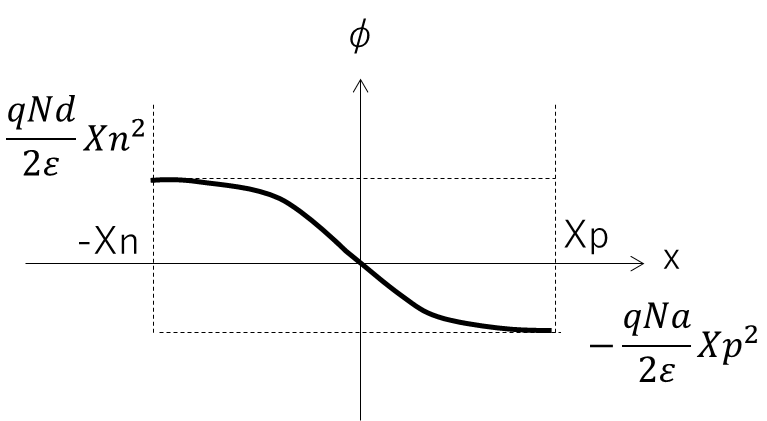
x=0でφ=0としなくても計算できるんですが、式が一番簡単になったので今回はこの形をとりました。
左側がN型領域、右側がP型領域ですが、もともとイメージしていた図とは左右反転しているように見えます。
これは、今回示しているのは電位の図だからです。
バンド図として描かれる場合、電子のエネルギーが高くなるほうを上にします。つまり、電位の図をx軸に対して上下反転すれば求めていたバンド図の形になります。
バンドの曲がりはEcもEvも一緒なので、PN接合全体のバンド図を改めて描き直すとこのようになります。
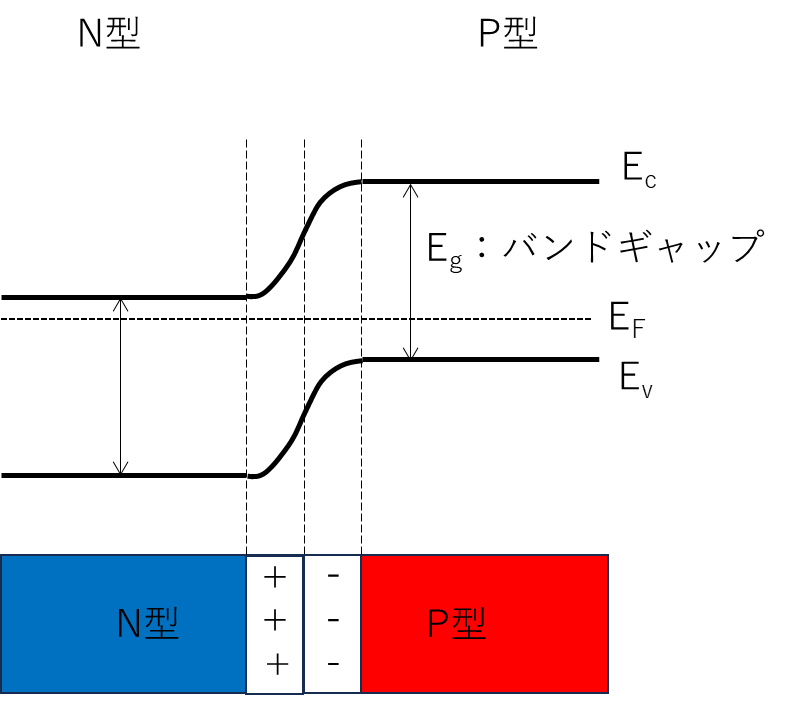
熱平衡時のPN接合のバンド図をちゃんと描くと、こんなイメージです。
図の曲線も、二次曲線に寄せて、手描きしていますが、少なくともP型とN型が直線で結ばれているわけではないことは、おわかりいただけると思います。
ここまでで、マクスウェル方程式からPN接合部のバンドが直線にならないことを解説しました。
実用上はPN接合で二次関数的にバンドが曲がると覚えておけばOK
厳密なことを考えるのであれば、マクスウェル方程式から電荷分布を考えて、電位を求めることはできます。
ただ、実用上毎回この作業を行うのは非現実的なので、熱平衡状態のPN接合を描くうえで、実用上押さえておけばいいポイントを3つ挙げます。
・なめらかな曲線で描く(直線ではない)
・空乏層領域と空乏層領域外のバンドは滑らかにつなぐ(微分可能な条件を満たす)
・P型とN型の境界部のバンドの傾きを一致させる(連続の条件を満たすため)
ヘテロ接合になると話は変わってきますが、一般的なシリコンのPN接合のバンド図を描くうえでは、上記3つの条件を満たしていれば、それほど外すことは無いと思います。
逆に、シリコンのPN接合のバンド図を描いた時に、3つの条件を外していると、違和感がある場合があります。
大学院入試でバンド図を描けと言われた場合、直線で描いていると×になる可能性もあるので、試験の場で描く必要がある方は気を付けて下さい。
順バイアス時と逆バイアス時に、電流ー電圧特性がどうなるかなどは、色々な本に書いてあるので、詳しくは書きません。ただ、空乏層近似をしたときに、バンドがなぜ曲がるのか?という点が書かれている記事はあまり見なかったので、今回書いてみました。
他のデバイスでも、需要があれば書いてみたいと思っています。
まとめ
この記事では、半導体を学ぶときに必ず出てくるエネルギーバンドについて、PN接合を作った時になぜ曲がるのかを簡単に解説しました。
「なぜ曲がるのか?」という問いに対しては、「空乏層に固定電荷があるから」というのが端的な答えになります。
固定電荷があると、マクスウェル方程式に当てはめて考えていくと、バンドが自然と曲がってしまうのです。
自分で描いていながら、半導体デバイスの基礎とされるPN接合も結構奥が深いものだと感じました。
このブログでは、半導体に関する記事を他にも書いています。半導体メモリ業界が中心ですが、興味がある記事があれば読んでみてください。

この記事はここまでです。最後まで読んでくださってありがとうございました。

コメント