みなさんこんにちは、このブログを書いている東急三崎口です。
この記事は、長期連載の第4回として、孤立原子のエネルギーと半導体の電気伝導について書いていきます。
本連載で扱っているのは、S.M.Sze著の半導体デバイス第2版の日本語訳verです。興味のある方は、下記リンク先から見てみてください。
前回の記事である、第3回はこちらです。
この記事のポイント
この記事で扱っているページおよび章は、下記のとおりです。
本記事で扱う内容と原著のぺージ
【内容】
・エネルギーと運動量
・金属、半導体、絶縁体における電気伝導
【ページ】
・p28-31
原子の結合やエネルギーバンドを扱うので、理工系の大学生レベルの基礎知識が必要になってきます。
できるだけ、基礎知識が無くても読めるように情報を追加して書いていますが、原著が前提にしている背景知識は理工系の大学生レベルなのでご了承ください。
【ポイント】
・エネルギーは運動量の二次関数で近似できる
・半導体の電気伝導は、金属と絶縁体の中間
エネルギーと運動量
さて、前回の第3回の内容で、孤立電子のエネルギーが出てきました。
導出過程は置いておいて、結果だけ書くとE=-13.6/n2 eVと書けます。
この孤立電子のエネルギー自体には、それほど大きな意味はありません。重要なところがあるとすれば、eV(エレクトロンボルト)という単位が出てくることです。
eVは、半導体のバンド理論を勉強するときに必ず出てくる単位です。日本語だと、「電子ボルト」と呼ぶこともありますが、エレクトロンボルト読みの方が主流だと思います。
eVの定義は簡単で、1つの電子に1Vの電圧をかけたときに発生するポテンシャルエネルギーです。
一般的には、エネルギーの単位はJ(ジュール)を使いますが、1eVをJで表示すると、1.6×10-19 Jとなります。
電子に着目しているので、Jで表示すると10-19がついていて、非常に小さな値になっているので、電子に対して電圧を加えたときのスケールに焼き直して、使いやすい数字としてあらわせるようにしているだけです。
このあと、バンドギャップの単位などにeVは嫌ほど出てくるので、電子の持っているエネルギーを表すにはeVを使うんだと思って覚えてしまった方が、今後出てくるバンド理論を学ぶ時に便利です。
そして、原著では自由電子のエネルギーが天下り的に書かれています。(p28)
これは、初学者の方には意味不明だと思います。いきなり、自由電子のエネルギーがE=p2/2m0として出てくるわけです。(E・p・m0はそれぞれ、E:自由電子のエネルギー、p:運動量、m0:自由電子の質量です。)
式の意味合いだけ見ると、エネルギーは運動量の二乗に比例して質量に反比例すると言えます。
この式の出どころをきっちり追おうとすると、量子力学をやらないといけないんですが、半導体のバンド構造を理解するうえでは、バンド中のエネルギーは運動量の二次関数として「近似できる」と考えておけば最初はさしつかえありません。
??と思われるかもしれませんが、二次関数として近似することの意味が、バンド構造を見るとわかります。
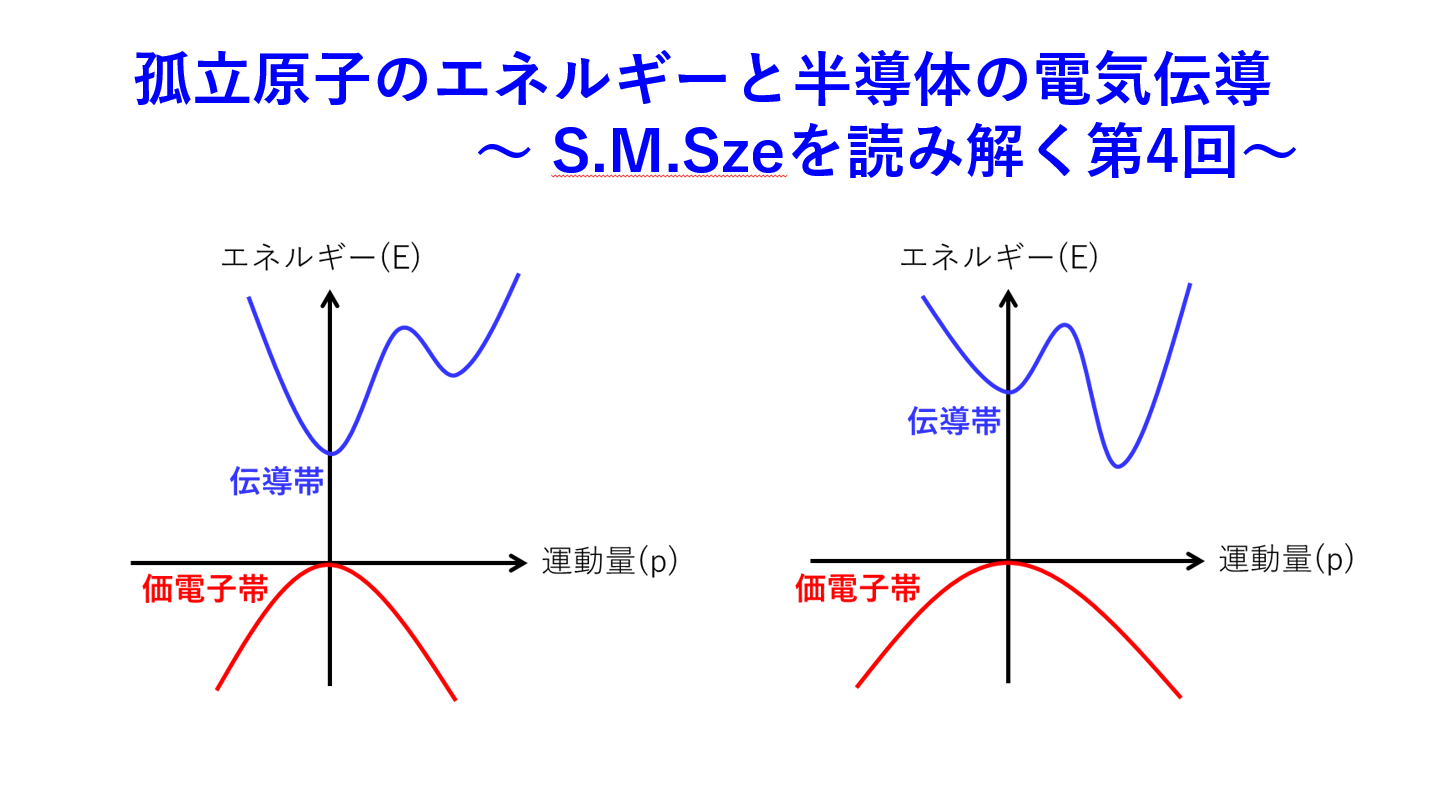
バンド構造の話になったので、天下り的に半導体のバンド構造を模式的に図にしています。
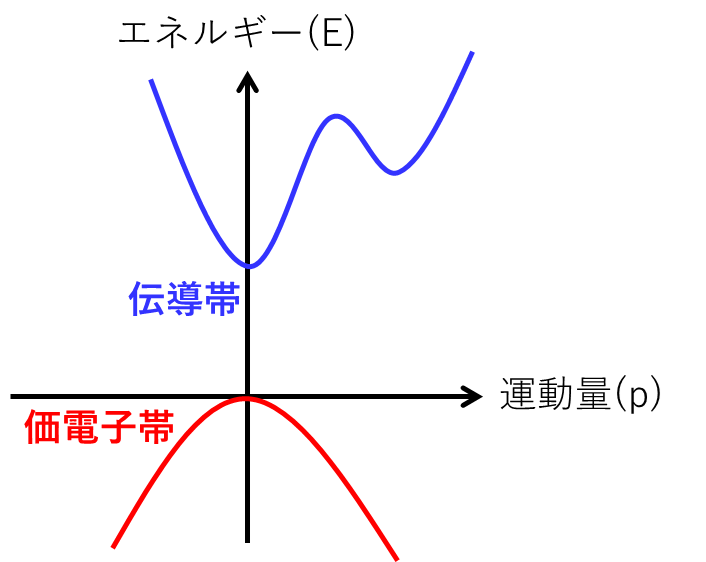
模式的に書いていますが、横軸を運動量、縦軸をエネルギーとして半導体のバンド構造を描くとこのようになります。
これが、なぜこうなるのか?ということに関しては、初学者の方は多分追えないので、こういうもんだと思ってください。(Siの格子の周期性から導かれるんですが、本気でやると大変なので、調べたい方はキッテルを読んでください。)
図の中で、「伝導帯」と「価電子帯」という言葉が出てきました。この2つの言葉は、バンド理論では常に出てくる用語なので、覚えてください。
バンド構造が描かれる時には、電子が埋まっている一番上のバンドと、電子が埋まっていない一番下のバンドが描かれます。(電子は、エネルギーが低いバンドから入るので、電子が埋まっている一番上のエネルギーがどこかにあります。)
半導体の場合、電子が埋まっている一番上のバンドが価電子帯で、電子が埋まっていない一番下のバンドが伝導帯となります。
半導体の伝導帯と価電子帯のそれぞれで注目するのは、「伝導帯の下端」と「価電子帯の上端」です。
伝導帯の下端と、価電子帯の上端は、図の中で示すとこんな感じです。

伝導帯の下端と、価電子帯の上端だけに着目すると、バンドの構造が二次関数に近い形をしているように見えないでしょうか。
半導体のバンド構造で、私たちが興味があるのは、伝導帯の下端と価電子帯の上端なので、この2つの部分が二次関数で近似できると都合がいいのです。
二次関数で近似できると都合がいいことに関しては、有効質量に踏み込むと意味合いがもう少しわかるんですが、ここでは有効質量までは踏み込まないことにします。(なぜなら、組成やバンド構造をいじる場合以外は、有効質量がいくつであるかは、あまり重要にならないからです。)
さて、エネルギーと運動量の話が長くなりましたが、半導体のバンド構造についてもう一つ知っておくべきことがあります。
伝導帯の下端と、価電子帯の上端が重要であることは、前に書いたとおりです。実は、半導体材料の種類によって、価電子帯の上端と、伝導帯の下端の運動量が一致している場合と一致していない場合があります。
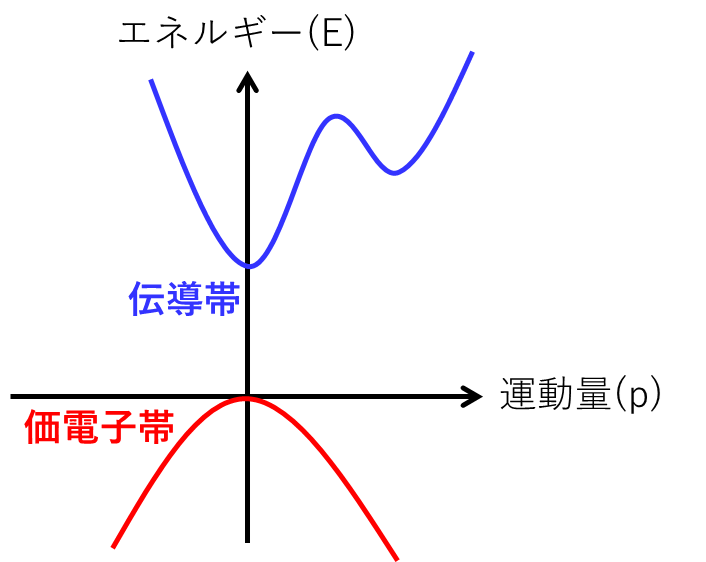
図に、2つのパターンを模式的に描いてみます。
価電子帯の上端と伝導帯の下端の運動量が一致している場合は、バンド図はこのようになります。(この場合、直接遷移型といいます。)
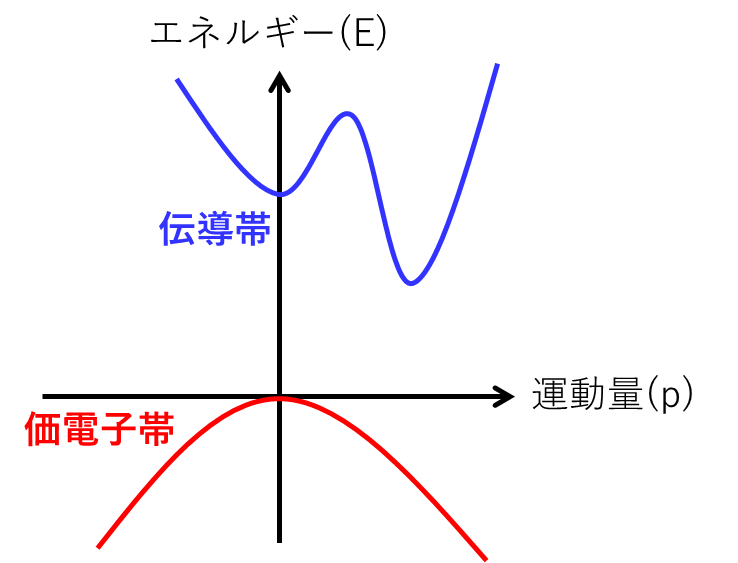
一方、価電子帯の上端と伝導帯の下端の運動量がずれている場合は、このようになります。(この場合、間接遷移型といいます。)
発光デバイスを考える時には、直接遷移型か間接遷移型かは非常に重要になります。
ただ、現時点では2つのパターンがあることを知っておけば十分です。
材料によって、直接遷移型か間接遷移型かは決まります。SiやGeは間接遷移型で、GaAsやGaNは直接遷移型です。
元素半導体は間接遷移が、化合物半導体は直接遷移が多い印象ですが、厳密にはバンド構造で決まっています。どちらのバンド構造かは、調べれば出てきます。
長々書いてしまいましたが、重要なポイントは半導体のバンドには価電子帯と伝導帯があり、バンド構造によって直接遷移型と間接遷移型があることです。
金属、半導体、絶縁体における電気伝導
原著のp30では、金属・半導体・絶縁体の電気伝導が触れられています。
金属・半導体・絶縁体は、電気の流れやすさが大きく違います。半導体は、金属と絶縁体の中間の電気伝導性だとよく言われます。
ただ、バンド構造としては、絶縁体と同じ構造をしています。(金属とは違います。)
金属と、半導体・絶縁体のバンド構造がどう違うかを簡単に図に示しています。
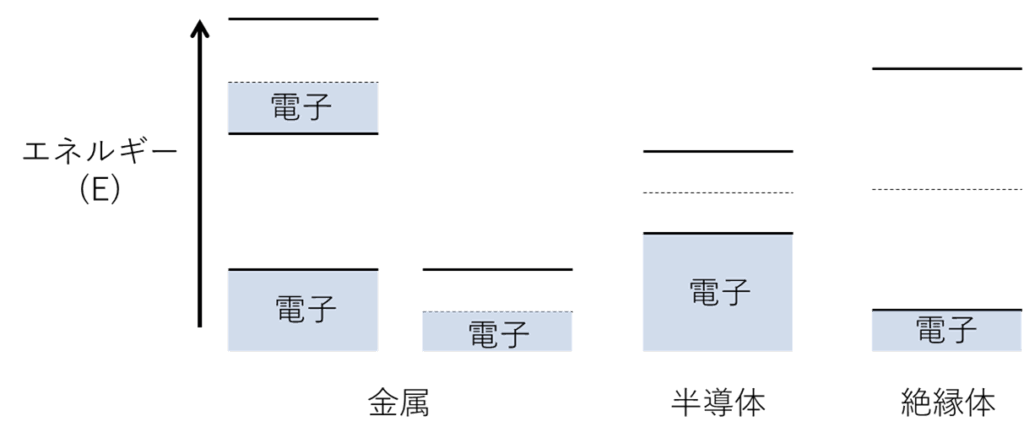
半導体のバンド構造でも出てきましたが、電子は原子の中で低いエネルギーから順番に席が埋まっていて、一番上の席まで通常は埋まっています。
電子の一番上の席の場所が、伝導帯の中の場合は金属になり、それ以外の場合は半導体や絶縁体となります。
この辺のバンド構造が具体的にどうなっていて、半導体は金属や絶縁体とどう違うのか?については、のちほど詳しく解説するので、ここでは簡単に金属・半導体・絶縁体のバンドの違いを模式的に描く程度にしておきます。
わからなかったら、わからなかったで構いません。
まとめ
この記事では、S.M.Szeを読み解く連載の第4回として孤立原子のエネルギーと半導体の電気伝導について書きました。
この連載では、S.M.Szeの内容について取り上げているので、わからない点や聞いてみたいことがあればQ&Aとして取り上げていきたいと思っています。コメント欄か、下記のお問い合わせフォームからご連絡いただければ、お返事いたします。
Q&Aは、本当に簡単なことでも構いません。例えば、
・半導体デバイスに、Siが使われている理由はなぜですか?
・3つ以上元素を組み合わせて化合物半導体をわざわざ作る理由は何?
など、内容は問いません。
ご意見・コメント等もお待ちしております。
前回の記事である、第3回はこちらです。

このブログでは、半導体に関する記事を他にも書いています。半導体メモリ業界が中心ですが、興味がある記事があれば読んでみてください。

この記事はここまでです。最後まで読んでくださってありがとうございました。

コメント