みなさんこんにちは、このブログを書いている東急三崎口です。
この記事では、半導体を学ぶうえで必ず出てくるバンド理論について、わかりやすく解説します。
半導体について勉強しようとすると、必ず出てくるのがバンド理論です。バンド理論をまじめに理解しようとすると、量子力学を勉強しないといけません。
量子力学は、理工系の大学に進んで物理系の学部に入ると勉強しないといけなくなります。ただ、実際に量子力学を学んだうえで半導体を学びたい方はそれほど多くないと思うので、細かい量子力学の内容抜きでバンド理論の枠組みを解説してきます。
バンド理論はなぜ出てくるのか
バンド理論が出てくるのは、金属・半導体・絶縁体の物理的な性質を理解するためです。金属・半導体・絶縁体について、バンド理論を使わずに解説した記事があるので、違いがわからないという方は読んでみてください。
最終的に理解したいのは半導体の構造なんですが、金属と半導体と絶縁体を統一的に理解できるので、バンド理論が使われます。
バンド理論を説明するときに、一般的に最初に出てくるのは水素原子のポテンシャルです。水素原子のポテンシャルを理解しようとすると、量子力学が出てきます。かつ、水素原子のポテンシャルをちゃんと理解しようとすると本を数冊読まないといけないんです。(本当は。)
正直なことを言うと、半導体を勉強していくうえで水素原子のポテンシャルが出てくるのはバンド理論の部分くらいなので、読み飛ばしてしまっても構わないです。ただ、最初に書いてあることがさっぱりわからなくて、挫折してしまうこともよくあるので、水素原子のポテンシャルに関しては触れずに解説していきます。
量子力学抜きでも知っておきたい前提条件
この記事では、水素原子のポテンシャルを扱わずにバンド理論を解説していくんですが、それでもいくつか知っておくべきことがあります。バンド理論を理解するうえで、知らないとどうしても話が進まないことを2つに絞って前提条件とします。
【どうしても必要な2つの前提条件】
・電子とホール
・エレクトロンボルト
電子とホール
どうしても避けては通れない前提条件の1つ目は、電子とホールです。
電子を一言で説明すると、「マイナスの電気を帯びた粒子」です。
電子を「粒子」と言い切っていいのか?と思われる方もいらっしゃるかもしれません。たしかに量子力学を考えると、電子は粒子と波動の二面性を持っていると説明されるので、電子を厳密に説明すると粒子と言い切るのは間違いです。ただ、半導体について学ぶ時には、(トンネル効果を扱わない限り)基本的にはマイナスの電気を帯びた粒子として扱われることが多いので、最初は粒子だと思ってください。
ホールは、電子と逆で「プラスの電気を帯びた粒子」です。
電子とホールを考えるのは、半導体だけです。金属について考える時には、電子だけで話が済んでしまいますし、絶縁体はそもそも電子もホールも無いと考えます。電子とホールの両方が登場するのは、半導体の一つの特徴です。
細かいことに関しては、実際にバンド理論を解説する部分で取り上げますが、電子やホールは電気を運ぶための「キャリア」と呼ばれます。電子やホールがあるから、電気を通すことができるんです。
聞き慣れない単位のエレクトロンボルト
2つ目に取り上げるのが、エレクトロンボルトです。
多分、エレクトロンボルトという言葉は、物理で半導体やバンド理論を使った専門分野を扱う人以外は、使わないのではないかと思います。
エレクトロンボルトというのは、エネルギーの単位です。よく「eV」といった形で書かれます。
定義は、1つの電子に1Vの電圧をかけたときに、電子が持つエネルギーです。
簡単に言うと、半導体の中に1Vの電圧をかけた時に、半導体の中にある電子は1eVのエネルギーを持つということです。
エネルギーの単位で一般的に使われるものは、ジュール(J)やカロリー(cal)があります。
eVをJで表すこともできるんですが、1eV=1.6×10-19Jになります。10-19がついているように、Jで表すと、非常に小さな値になってしまって、使いにくいんです。なので、簡単な数字になるようにeVを使います。最初は違和感があると思いますが、慣れてくるとeVの方が直感的に理解しやすい単位になっていることがわかるようになりますよ。
量子力学を抜きに半導体のバンド理論を考える
さて、ここから量子力学を抜きに半導体のバンド理論を解説していきます。
まず、金属・半導体・絶縁体のバンド構造を書くと、このようになっています。

量子力学を抜きにバンド構造を考えると、大きく分けて金属と半導体・絶縁体でバンド構造が大きく違います。
1つずつ解説していきます。
伝導帯と価電子帯
まずは、伝導体と価電子帯がいきなり出てきました。物質の中には、電子が必ずいます。物質には、電子が存在できるエネルギー帯と存在できないエネルギ―帯があります。(厳密な説明には量子力学が必要ですが、物質をミクロに見ると電子が取れるエネルギーはとびとびの値を取ることが知られています。原子1つだけで見ると、電子が取れるエネルギーは飛び飛びの値を取るんですが、原子が無数に集まると飛び飛びの値が少し幅を持ったバンドになります。)
電子はエネルギーの低いバンドから順々に席が決まっていて、原子によって決まっている一番上の席まで埋まっていきます。
電子が入れる一番上の席(一番エネルギーが高いところ)まで埋まった時のことを考えます。
一番上の席よりちょっとだけ高いエネルギーが、電子が存在してもいいバンドなのか、存在できないバンドなのかで話が変わってきます。一番上の席よりちょっとだけ高いエネルギーが、電子が存在してもいいバンドの場合、金属になります。
一方、一番上の席よりちょっとだけ高いエネルギーが電子が存在できないバンドの場合、半導体か絶縁体になります。
そして、電子が入れる一番上の席よりもちょっとだけ高いエネルギーの領域に電子が動くと、電子は自由に動けるようになります。(それまでは、原子同士の結合に縛られていて、自由に動くことはできませんした。)
自由に動くことができる電子(自由電子と言います)がたくさんあると、自由に動ける電子が電気を伝えることができます。
金属は、電子が入れる一番上の席よりちょっとだけ高いエネルギーでも電子が存在できるので、電気をよく流すわけです。
一方、半導体や絶縁体は電子の一番上の席よりちょっとだけ高いエネルギーは、電子が存在できないエネルギーになっています。ちょっとだけ高いエネルギー領域は電子が存在できないんですが、ちょっとずつエネルギーを上げていくと電子が存在できる領域になります。この領域を伝導帯といいます。
そして、電子が入れる一番上の席より下のエネルギー領域を価電子帯といいます。価電子帯と伝導体の間のエネルギーには、半導体や絶縁体にはギャップがあります。このギャップのことを、バンドギャップと言います。
私たちが生活している環境だと、だいだい数十℃の温度なので、このくらいの温度域である程度より小さいバンドギャップをもつ物質を半導体といい、大きいバンドギャップを持つ物質を絶縁体と言います。
つまり、半導体と言われる材料は私たちが生活している環境で、ちょうどいいバンドギャップを持つ物質なわけです。
バンドギャップとは何者なのか?
次に着目するのが、バンドギャップとは何者なのか?ということです。
最初にバンド理論を学ぼうとすると、伝導帯・価電子帯もそうですが、バンドギャップの存在を不思議に感じることがあります。
なぜバンドギャップがあるのか?という問いの答えは、量子力学を学ばないと出てきません。(量子力学の前提にあるのは、すべての電子が取れるエネルギーは飛び飛びの値を取るという考え方です。このことを、エネルギーの量子化と言いますが、量子化を原子レベルで適用していくと、バンドギャップが出てきます。)
簡単に考えるなら、バンドギャップのエネルギーの中には電子は存在できないと考えてください。
そして、半導体を議論するときに、バンドギャップがeVで出てくることがよくあります。例えば、半導体によく使われているシリコンのバンドギャップは1.1eV程度です。(厳密に言うと、バンドギャップは温度や不純物の量で変わりますが、今回は不純物が含まれていない純粋なシリコンで室温付近の状態のバンドギャップを示しています。)
バンドギャップを1.1eVというわかりやすい数字で表せるのが、エレクトロンボルトを使うメリットです。
パワー半導体向けに、ワイドバンドギャップ半導体と呼ばれるものが研究されていますが、ワイドバンドギャップというのは、シリコンの1.1eVよりもバンドギャップが大きいもののことを言っています。
(パワー半導体でバンドギャップが大きい材料を使う理由については、バンドギャップについて理解するとよくわかりますが、別の記事で解説することにします。)
バンドギャップに関しては、最初に半導体を学ぶ時には、「そういうものなんだ」と思って先に進んだ方が賢明です。
シリコンに関わらず、バンドギャップの存在自体を受け入れて先に進んでも、半導体の理解に支障はありません。(研究機関で働いている人や、半導体デバイス設計の仕事をするのであれば話は別ですが。)
フェルミ準位を理解する
バンドギャップについて解説したので、もう少し詳しく半導体のバンド構造を見ていきます。
半導体のバンド構造は、詳しく書くとこのようになっています。
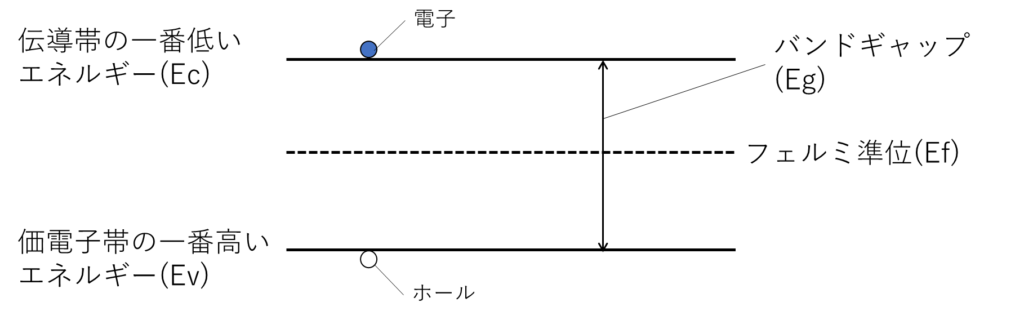
先ほどの解説では、価電子帯と伝導帯と書きましたが、厳密に書くと、伝導帯の一番低いエネルギーと価電子帯の一番高いエネルギーの差がバンドギャップです。
価電子帯の一番高いエネルギーをEv、伝導帯の一番低いエネルギーをEc、バンドギャップをEgと略すことがよくあります。
(価電子帯・伝導帯は英語で書くとそれぞれ、Valence Band・Conduction Bandと書きます。英語表記の頭文字を取って、EvやEcとなっているわけです。)
新しい用語で、フェルミ準位(Ef)が出てきました。
このフェルミ準位というのが、半導体のバンド理論の中で理解するのが難しいところです。
フェルミ準位を簡単に説明すると、「電子の存在確率が50%になるエネルギー」です。
ここで2つの疑問が出てきます。
1つ目は、電子の存在確率が50%になるエネルギーに何の意味があるのか?ということ。
2つ目は、フェルミ準位がバンドギャップの中にあるのはなぜ?ということです。
電子の存在確率が50%になるエネルギーに、何の意味があるのかということについては、今後わかるようになります。というのは、半導体は純粋なものであればバンドギャップの中間にフェルミ準位が来ます。
しかし、実際に半導体を使う場合には、純粋な半導体とは別に不純物を加えて極性や電気の流れやすさをコントロールします。不純物を入れると、フェルミ準位の位置が動くんですよ。フェルミ準位の位置が動くと考えることで、半導体デバイスの動作を理解しやすくなります。最初のうちは、フェルミ準位もそんなもんかと思ってください。
2つ目の、フェルミ準位がバンドギャップの中にあるのはなぜか?ということについては、少し突っ込んで考えていかないといけません。
半導体に不純物を入れていない場合、基本的にはバンドギャップがあるので、伝導帯には電子は存在しないはずです。
しかし、室温でもごくわずかにバンドギャップを超えるキャリア(電子とホールのことを合わせてキャリアと言います)が存在し、伝導帯には電子が、価電子帯にはホールが存在します。室温で不純物を入れていない半導体が、電流を流すのはごくわずかに存在する電子とホールが電気を流しているからです。
そして、ごくわずかにバンドギャップを超えるキャリアが存在するので、電子の存在確率が50%になるエネルギーがバンドギャップの中にあるんです。
このことに関しては、半導体物性の本を読むと、状態密度関数・フェルミディラック分布関数・マクスウェルボルツマン分布を使って理由が書いてあるので、どうしても詳しく知りたい方は読んでみてください。(多分読む気にならないくらい、積分や近似が使われていると思いますが。)
今回は、積分や近似を使うことをできるだけ省いて解説しているので、細かい部分は省きますが、一応半導体物理は、数学的なモデル化も非常に細かくされているので、興味があれば見てみると面白いと思います。(少なくとも、高校数学はもちろんのこと、大学の学部生で学ぶレベルの数学を知らないと読み解けないですが。)
不純物を入れるとどうなるか
ここまで、半導体のバンド理論をできるだけ数式を使わずに解説してきました。
実は、ここまでの半導体の前提として、書いていませんでしたが、純粋な半導体について書いてきました。純粋な半導体というのは、不純物を一切入れていない半導体のことです。
しかし、実際に半導体を使って電子デバイスを作る時には、不純物の量をコントロールすることで、デバイスを作っていきます。不純物を入れると、ここまで説明してきた中では、フェルミ準位が変わってきます。
フェルミ準位が変わって、実際どうなるのかということに関しては、PN接合を解説するときにまとめて取り上げることにします。
基本的な物性は材料で決まる
半導体を理解するためのバンド理論について解説してきました。
例えば、シリコンであれば室温で1.1eV程度のバンドギャップを変えたいと思ったら、どうしたらいいのでしょうか。
実は、バンドギャップは温度や不純物の量で多少は変わりますが、劇的に変えることはできません。
バンドギャップは、物質固有の値になるので、シリコンを使っていれば基本的に1.1eVのバンドギャップを持ちます。
バンドギャップを変えたい場合には、使う材料を変えるしかないのが実際のところです。
パワー半導体に興味がある方であれば、SiCやGaNなど、Si以外の半導体が使われていることを目にすることも多いと思います。SiCやGaNなどの材料が使われているのは、Siよりバンドギャップが大きい半導体材料を使おうとしているからです。
まとめ
この記事では、半導体を学ぶうえで必ず出てくるバンド理論について、半導体にフォーカスして解説しました。
半導体物性の本を読むと、量子力学の考え方ありきで書かれていたり、積分などの数式をもとに解説されていたりして、読むのに挫折しがちな部分です。
半導体の物性を研究していたり、半導体デバイスを設計している人であれば話は別ですが、そうでない人に量子力学まで理解しろというのは無理だろうと思って、できるだけ数式に頼らずに解説しています。
わからない部分や間違い・ご意見等がありましたら、お気軽にコメントくださいませ。
このブログでは、半導体に関する記事を他にも書いています。半導体メモリ業界が中心ですが、興味がある記事があれば読んでみてください。

この記事はここまでです。最後まで読んでくださってありがとうございました。


コメント